2.6. Consistency Test
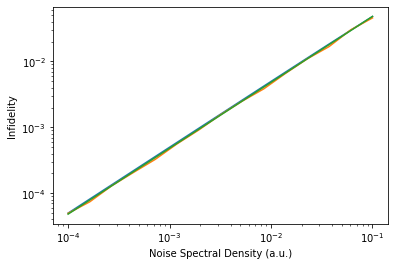
To demonstrate the consistency of the different noise simulation methods, we calculate the impact of white noise with the Monte Carlo method, a Lindblad master equation and generalized filter functions.
The qubit under consideration is a singlet-triplet semiconductor qubit with the Hamiltonian:
\begin{equation}
H = \frac{J + \delta J}{2}\sigma_z + E_z \sigma_x
\end{equation}
where \(J\) is the exchange energy, \(E_z\) the zeeman-splitting and \(\delta J\) is white noise.
We start without additional control \(J=0\) and create helper functions for the calculation of infidelities with various methods.
[1]:
from qopt import *
import numpy as np
import matplotlib.pyplot as plt
def create_lindblad_solver(n_time_steps, noise_variance, total_time,
bz_rotation):
delta_bz = bz_rotation / total_time
delta_t = total_time / n_time_steps
def prefactor_function(transferred_parameters, _):
return noise_variance * np.ones_like(transferred_parameters)
lindblad_solver = LindbladSolver(
h_drift=[delta_bz * .5 * DenseOperator.pauli_x()],
h_ctrl=[.5 * DenseOperator.pauli_z()],
tau=delta_t * np.ones(n_time_steps),
prefactor_function=prefactor_function,
lindblad_operators=[.5 * DenseOperator.pauli_z()]
)
return lindblad_solver
def evaluate_infidelity_fid_lindblad(n_time_steps, noise_variance,
total_time, bz_rotation):
lindblad_solver = create_lindblad_solver(
n_time_steps, noise_variance, total_time, bz_rotation)
fid_ctrl_amps = np.expand_dims(np.zeros(n_time_steps), 1)
target = (.5 * DenseOperator.pauli_x()).exp(1j * bz_rotation)
lindblad_cost_fkt = OperationInfidelity(
solver=lindblad_solver,
super_operator_formalism=True,
target=target
)
lindblad_solver.set_optimization_parameters(fid_ctrl_amps)
return lindblad_cost_fkt.costs()
def create_mc_solver(n_time_steps, noise_variance, total_time, bz_rotation,
low_freq_ex):
delta_bz = bz_rotation / total_time
delta_t = total_time / n_time_steps
def noise_spectral_density(f):
return 2 * noise_variance * np.ones_like(f) # factor of 2 for
# one-sided spectrum
noise_trace_generator = NTGColoredNoise(
n_samples_per_trace=n_time_steps,
dt=delta_t,
noise_spectral_density=noise_spectral_density,
n_traces=1000,
low_frequency_extension_ratio=low_freq_ex
)
# The low frequency extension leads to the sampling of a noise trace
# for more time steps. The simulation then uses only a section of this
# longer trace. The extension allows the noise trace generator to include
# low frequency noise.
monte_carlo_solver = SchroedingerSMonteCarlo(
h_drift=[delta_bz * .5 * DenseOperator.pauli_x()],
h_ctrl=[.5 * DenseOperator.pauli_z()],
tau=delta_t * np.ones(n_time_steps),
h_noise=[.5 * DenseOperator.pauli_z()],
noise_trace_generator=noise_trace_generator
)
return monte_carlo_solver
def evaluate_fidelity_fid_mc(
n_time_steps, noise_variance, total_time, bz_rotation, low_freq_rel):
monte_carlo_solver = create_mc_solver(
n_time_steps, noise_variance, total_time, bz_rotation, low_freq_rel)
fid_ctrl_amps = np.expand_dims(np.zeros(n_time_steps), 1)
target = (.5 * DenseOperator.pauli_x()).exp(1j * bz_rotation)
mc_cost_fkt = OperationNoiseInfidelity(
solver=monte_carlo_solver,
target=target,
neglect_systematic_errors=False
)
monte_carlo_solver.set_optimization_parameters(fid_ctrl_amps)
return mc_cost_fkt.costs()
def create_ff_solver(n_time_steps, total_time, bz_rotation):
delta_bz = bz_rotation / total_time
delta_t = total_time / n_time_steps
ff_hamiltonian_noise =[[
.5 * DenseOperator.pauli_z().data,
np.ones(n_time_steps),
'noise Source 1'
], ]
ff_solver = SchroedingerSolver(
h_drift=[delta_bz * .5 * DenseOperator.pauli_x()],
h_ctrl=[.5 * DenseOperator.pauli_z()],
tau=delta_t * np.ones(n_time_steps),
filter_function_h_n=ff_hamiltonian_noise
)
return ff_solver
def evaluate_ff_infid(n_time_steps, noise_variance, total_time, bz_rotation,
low_freq_rel):
ff_solver = create_ff_solver(n_time_steps, total_time, bz_rotation)
fid_ctrl_amps = np.expand_dims(np.zeros(n_time_steps), 1)
def noise_spectral_density(f):
return 2 * noise_variance * np.ones_like(f) # factor of 2 for
# one-sided spectrum
ff_cost_fkn = OperatorFilterFunctionInfidelity(
solver=ff_solver,
noise_power_spec_density=noise_spectral_density,
omega=(1 / (total_time * low_freq_rel)) *
(np.arange(n_time_steps * low_freq_rel) + 1)
)
ff_solver.set_optimization_parameters(fid_ctrl_amps)
return ff_cost_fkn.costs()
We calculate the infidelities as function of the noise strength.
[2]:
total_time = 2
n_variance_values = 15
noise_variance_values = np.logspace(
-4, -1, n_variance_values, dtype=float, endpoint=True, base=10)
mc_infidelities = np.zeros(n_variance_values)
lindblad_infidelities = np.zeros(n_variance_values)
ff_infidelities = np.zeros(n_variance_values)
for i, noise_variance in enumerate(noise_variance_values):
lindblad_infidelities[i] = evaluate_infidelity_fid_lindblad(
n_time_steps=30, noise_variance=noise_variance, total_time=total_time,
bz_rotation=np.pi
)
mc_infidelities[i] = evaluate_fidelity_fid_mc(
n_time_steps=30, noise_variance=noise_variance, total_time=total_time,
bz_rotation=np.pi, low_freq_rel=10)
ff_infidelities[i] = evaluate_ff_infid(
n_time_steps=30, noise_variance=noise_variance, total_time=total_time,
bz_rotation=np.pi, low_freq_rel=10
)
Plotting the infidelities reveals that the results only deviate by a few percent.
[3]:
plt.plot(noise_variance_values, lindblad_infidelities, label='Lindblad')
plt.plot(noise_variance_values, mc_infidelities, label='Monte Carlo')
plt.plot(noise_variance_values, ff_infidelities, label='Filter Functions')
plt.xscale('log')
plt.ylabel('Infidelity')
plt.yscale('log')
plt.xlabel('Noise Spectral Density (a.u.)')
[3]:
Text(0.5, 0, 'Noise Spectral Density (a.u.)')