2.7. Phase Noise with Filter Functions
In this section we discuss how to use filter functions to study the effect of amplitude, frequency and also phase noise on a resonantly driven qubit. We start by discussing the coherent dynamics and then add filter function.
2.7.1. Coherent Dynamics
We consider a single qubit with a resonant drive source. The Hamiltonian in the lab frame is given as:
where \(\omega_0\) is the resonance frequency of the qubit, \(A(t)\) is the time-depended driving amplitude, \(\omega\) is the driving frequency and \(\phi(t)\) is the time-depended phase of the driving signal. We transform the Hamiltonian into the rotating frame and apply the rotating wave approximation to yield:
We assume resonant control \(\omega - \omega_0 = 0\). To bring the Hamiltonian into the standard form \(H_c = \sum_k u_k C_k\) we identify:
[1]:
import matplotlib.pyplot as plt
from qopt import *
import numpy as np
import filter_functions as ff
n_time_steps = 10
delta_t = 1
h_ctrl = [DenseOperator.pauli_x(), DenseOperator.pauli_y()]
def amplitudes(opt_pars):
# This amplitude function does not need to alter the shape of the input.
ctrl_amplitudes = np.empty_like(opt_pars)
# x-control
ctrl_amplitudes[:, 0] = opt_pars[:, 0] * np.cos(opt_pars[:, 1])
# y-control
ctrl_amplitudes[:, 1] = opt_pars[:, 0] * np.sin(opt_pars[:, 1])
return ctrl_amplitudes
To use analytical gradients, we also need the derivatives of our control amplitudes by the optimization parameters \(v_1(t) = A(t)\) and \(v_2(t)=\phi(t)\):
[2]:
def amplitude_derivatives(opt_pars):
derivatives = np.empty(shape=([n_time_steps, 2, 2]), dtype=float)
# derivatives by the amplitude
derivatives[:, 0, 0] = np.cos(opt_pars[:, 1])
derivatives[:, 0, 1] = np.sin(opt_pars[:, 1])
# derivatives by the phase
derivatives[:, 1, 0] = -1 * opt_pars[:, 0] * np.sin(opt_pars[:, 1])
derivatives[:, 1, 1] = opt_pars[:, 0] * np.cos(opt_pars[:, 1])
return derivatives
2.7.2. Noisy Dynamics
We want to consider noise on the amplitude \(A \rightarrow A + \delta A\), frequency \(\omega \rightarrow \omega + \delta \omega\) and on the phase \(\phi \rightarrow \phi + \delta \phi\). To bring the Hamiltonian into the form \(H = H_c + H_n\) with seperated control Hamiltonian \(H_c\) and noise Hamiltonian \(H_n\), we perform a Taylor-Expansion and neglect terms beyond the first order.
Please note that \(\delta \omega\) can equally be used to describe noise on the resonant frequency of the qubit or the frequency of the driving system.
Harrison Ball et al. applied a first order approximation to the phase noise \(\phi(t) \approx \dot{\phi}t\), such they could regard it as additional perturbation to the driving frequency in https://doi.org/10.1038/npjqi.2016.33. Here we want to keep the full phase noise dynamics.
We need to bring the noise Hamiltonian into the form
and thus we identify:
In the implementation of the noise Hamiltonian for the filter functions, we can reuse the derivatives from the amplitude function:
ATTENTION: The solver sets the order of noise parameters with the order given in the parameter filter_function_h_n. This order must be respected when setting the derivatives and the noise spectral densitites.
[3]:
def filter_function_h_n(opt_pars, tr_pars, ctrl_amps):
deriv_ctrl_amps_by_opt_pars = amplitude_derivatives(opt_pars)
return [[
.5 * DenseOperator.pauli_x(),
deriv_ctrl_amps_by_opt_pars[:, 0, 0],
'Amplitude Noise 1'
],
[
.5 * DenseOperator.pauli_y(),
deriv_ctrl_amps_by_opt_pars[:, 0, 1],
'Amplitude Noise 2'
],
[
.5 * DenseOperator.pauli_x(),
deriv_ctrl_amps_by_opt_pars[:, 1, 0],
'Phase Noise 1'
],
[
.5 * DenseOperator.pauli_y(),
deriv_ctrl_amps_by_opt_pars[:, 1, 1],
'Phase Noise 2'
],
[
.5 * DenseOperator.pauli_z(),
np.ones(n_time_steps),
'Frequency Noise'
],
]
Next, we need the derivatives of the noise susceptibilities by the control amplitudes. And employ the chain rule for this purpose:
with
[4]:
def filter_function_n_coeffs_deriv(opt_pars, tr_pars, ctrl_amps):
# start with the derivatives of the noise susceptibilities by the
# optimizaiton parameters
deriv_susceptibilities_by_opt_pars = np.zeros(
shape=[opt_pars.shape[0], 5, 2], dtype=float)
# derivatives by the Amplitude
deriv_susceptibilities_by_opt_pars[:, 2, 0] = -1 * np.sin(opt_pars[:, 1])
deriv_susceptibilities_by_opt_pars[:, 3, 0] = np.cos(opt_pars[:, 1])
# derivatives by the phase
deriv_susceptibilities_by_opt_pars[:, 0, 1] = \
deriv_susceptibilities_by_opt_pars[:, 2, 0]
deriv_susceptibilities_by_opt_pars[:, 1, 1] = \
deriv_susceptibilities_by_opt_pars[:, 3, 0]
deriv_susceptibilities_by_opt_pars[:, 2, 1] = \
-1 * opt_pars[:, 0] * np.cos(opt_pars[:, 1])
deriv_susceptibilities_by_opt_pars[:, 3, 1] = \
-1 * opt_pars[:, 0] * np.sin(opt_pars[:, 1])
# Then we calculate the derivatives of the optimization parameters by the
# control amplitudes,
# by first calculating the partial derivatives of the control amplitudes
# by the optimizaiton parameters:
deriv_ctrl_amps_by_opt_pars = amplitude_derivatives(opt_pars)
# we transpose to yield the shape(n_time, n_ctrl_amps, n_opt_pars)
deriv_ctrl_amps_by_opt_pars = np.transpose(deriv_ctrl_amps_by_opt_pars,
axes=[0, 2, 1])
# and then calculating the inverse.
deriv_opt_pars_by_ctrl_amps = np.linalg.inv(deriv_ctrl_amps_by_opt_pars)
# finally we can calculate the desired derivatives
deriv_susceptibilities_by_ctrl_amps = np.einsum(
'tsv,tvu->sut',
deriv_susceptibilities_by_opt_pars,
deriv_opt_pars_by_ctrl_amps
)
# the final shape is chosen as required by the filter_functions_package
return deriv_susceptibilities_by_ctrl_amps
Next we can put everything together to create the solver:
[5]:
amplitude_function = CustomAmpFunc(
value_function=amplitudes,
derivative_function=amplitude_derivatives
)
solver = SchroedingerSolver(
h_drift=[0 * DenseOperator.pauli_x()],
h_ctrl=h_ctrl,
tau=delta_t*np.ones(n_time_steps),
amplitude_function=amplitude_function,
filter_function_h_n=filter_function_h_n,
filter_function_n_coeffs_deriv=filter_function_n_coeffs_deriv
)
We can check the implementation of the coherent dynamics with a simple pulse:
[6]:
x_pi_half_gate_pulse = np.zeros(shape=(n_time_steps, 2), dtype=float)
x_pi_half_gate_pulse[:, 0] = .25 * np.pi / (n_time_steps * delta_t)
x_pi_half_gate_pulse[:, 1] = .5 * np.pi
solver.set_optimization_parameters(x_pi_half_gate_pulse)
solver.plot_bloch_sphere()
To get interesting filter functions, we generate a random pulse:
[7]:
np.random.seed(4)
random_pulse = np.zeros(shape=(n_time_steps, 2), dtype=float)
random_pulse[:, 0] = np.random.rand(n_time_steps) * np.pi / (n_time_steps * delta_t)
random_pulse[:, 1] = 1 * np.random.rand(n_time_steps) * np.pi
solver.create_pulse_sequence(random_pulse)
pulse_sequence = solver.pulse_sequence
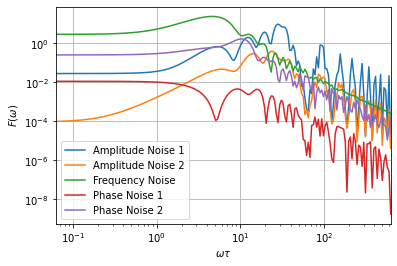
omega = ff.util.get_sample_frequencies(
pulse_sequence, n_samples=200, spacing='log')
_ = ff.plotting.plot_filter_function(pulse_sequence, omega, yscale='log')
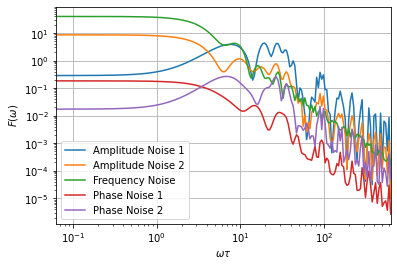
Now we define a noise spectral density. In our model, we assume that the amplitude is subjected to \(1/f\) type noise, the phase is subjected to white noise and the frequency is subjected to \(1/f^2\) noise.
We verify that everything is set up correctly by calculating the cost functions and compare the analytic to numeric derivatives calculated by finite differences.
[8]:
def psd(f):
spectral_power_density = np.zeros(shape=[5, f.shape[0]], dtype=float)
# 1/f noise on the amplitudes
spectral_power_density[0, :] = .01 / f
spectral_power_density[1, :] = .01 / f
# white noise on the phase
spectral_power_density[2, :] = .1
spectral_power_density[3, :] = .1
# 1/f^2 noise on the frequency
spectral_power_density[4, :] = .0001 / f ** 2
return spectral_power_density
ff_infidelity = OperatorFilterFunctionInfidelity(
solver=solver,
noise_power_spec_density=psd,
omega=omega
)
target_gate = DenseOperator.pauli_x().exp(-1j * .25 * np.pi)
coherent_infid = OperationInfidelity(
solver=solver,
target=target_gate
)
simulator = Simulator(
solvers=[solver, ],
cost_funcs=[coherent_infid, ff_infidelity]
)
print('Infidelities calculated with filter function:')
print(simulator.wrapped_cost_functions(random_pulse))
print('Absolute and relative deviation of analytic and numeric gradients.')
print(simulator.compare_numeric_to_analytic_gradient(random_pulse))
Infidelities calculated with filter function:
[0.81526447 0.00651779 0.02648523 0.00099263 0.00440001 0.04920558]
Absolute and relative deviation of analytic and numeric gradients.
(3.676565430814301e-08, 1.9975541347967917e-08)
In a last step, we can start an optimization. We set the cost_func_weights to give the infidelitites calculated with the filter functions a higher weight of two orders of magnitude. This is sometimes necessary to avoid, that the optimizer simply optimizes the coherent dynamics and then gets stuck in a local optimum.
[9]:
optimizer = ScalarMinimizingOptimizer(
system_simulator=simulator,
cost_func_weights=[1, 1e2, 1e2, 1e2, 1e2, 1e2]
)
result = optimizer.run_optimization(random_pulse)
data_container = DataContainer()
data_container.append_optim_result(result)
analyser = Analyser(data_container)
analyser.plot_costs()
[9]:
<AxesSubplot:xlabel='Iteration', ylabel='Costs'>
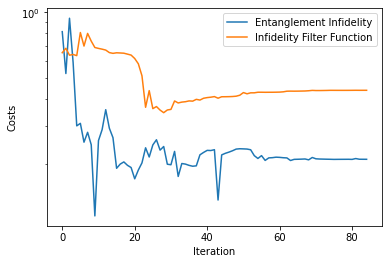
In a last step, we restart the optimization without weights to calibrate coherent errors. As initial pulse, we use the optimized pulse from the last optimization.
[10]:
optimizer.cost_func_weights = None
result_2 = optimizer.run_optimization(result.final_parameters)
data_container.append_optim_result(result_2)
analyser.plot_costs(n=1)
solver.plot_bloch_sphere(result_2.final_parameters)
solver.create_pulse_sequence(result_2.final_parameters)
pulse_sequence = solver.pulse_sequence
_ = ff.plotting.plot_filter_function(pulse_sequence, omega, yscale='log')
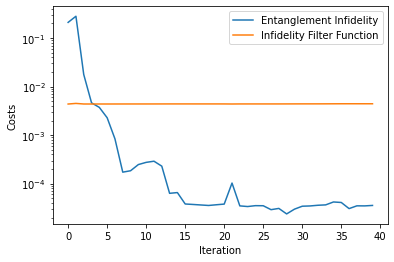
[10]: